INTRODUCTION:

Orbital mechanics, the study of the motion of objects in space, has come a long way since the days of Johannes Kepler. From the early understanding of planetary orbits to the precise navigation systems of today, orbital mechanics has played a crucial role in our exploration of the universe. In this blog post, we’ll take a journey through the evolution of orbital mechanics, highlighting key milestones, breakthroughs, and practical applications.
The Early Days: Kepler’s Laws
In the early 17th century, a brilliant German mathematician and astronomer named Johannes Kepler transformed our understanding of the cosmos with his groundbreaking discoveries about planetary motion. His three fundamental laws of planetary motion, known as Kepler’s Laws, describe how planets orbit the Sun and laid the foundation for modern astronomy and orbital mechanics.
Kepler’s First Law: The Law of Ellipses
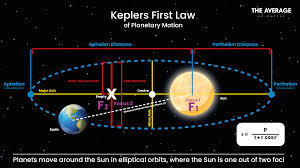
Kepler’s First Law states that all planets move in elliptical orbits with the Sun located at one of the two foci of the ellipse.
What does this mean? Imagine an ellipse as a stretched-out circle. If you think of a planet’s orbit, it’s not a perfect circle but rather an oval shape. This was a significant shift from the earlier belief that planets moved in perfect circles.
Example: Picture a racetrack. If you were running on an oval track, your path would be longer when you are on the outer edge compared to running in a circle. Similarly, planets like Earth travel along an elliptical path around the Sun, which means their distance from the Sun changes throughout their orbit.
Kepler’s Second Law: The Law of Equal Areas
Kepler’s Second Law states that the line connecting a planet to the Sun sweeps out equal areas in equal times. This means that as a planet travels along its elliptical path, it moves faster when it is closer to the Sun and slower when it is farther away.
Why is this important? This law helps explain why planets speed up as they approach the Sun (at a point called perihelion) and slow down as they move away (at a point called aphelion).
Example: Think of riding a swing. When you pull back and then let go, you swing forward quickly at first, but as you reach the highest point on the other side, you slow down before coming back down. In a similar way, planets speed up when they are nearer to the Sun and slow down when they are farther away.
Kepler’s Third Law: The Law of Harmonies
Kepler’s Third Law states that the square of a planet’s orbital period (the time it takes to complete one orbit) is directly proportional to the cube of its semi-major axis (the longest radius of its elliptical orbit).
In simpler terms, this law shows that there is a consistent relationship between how far a planet is from the Sun and how long it takes to orbit it. The farther a planet is from the Sun, the longer it takes to complete one full orbit.
Example: Imagine two friends racing around a track. If one friend runs on an inner lane (closer to the center), they will finish their lap faster than another friend who is running on an outer lane (farther from the center). Similarly, planets closer to the Sun—like Mercury—have shorter orbital periods than those farther out—like Neptune.
The Impact of Kepler’s Laws
Kepler’s laws were revolutionary because they provided a mathematical framework for understanding how celestial bodies move through space. They challenged long-held beliefs about circular orbits and laid crucial groundwork for future astronomers and physicists.
Want To Know More About:
Unlock the wonders of the sky and beyond—shop the best telescopes, binoculars, and drones today:

Newton’s Law of Universal Gravitation

In 1687, Sir Isaac Newton made a monumental contribution to science with his work “Philosophiæ Naturalis Principia Mathematica,” where he introduced the Law of Universal Gravitation. This law fundamentally changed our understanding of how objects in the universe interact with each other through gravity.
What is the Law of Universal Gravitation?
Newton’s Law of Universal Gravitation states that every point mass attracts every other point mass in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
In simpler terms, this means:
- More Mass = More Attraction: The greater the mass of an object, the stronger its gravitational pull. For example, Earth has a much larger mass than a small rock, which is why the rock falls toward Earth when dropped.
- More Distance = Less Attraction: The farther apart two objects are, the weaker the gravitational force between them. If you imagine two magnets, they attract each other more strongly when they are close together than when they are far apart.
The Gravitational Force Equation
Newton summarized this relationship in a formula:
$$
F = G \frac{m_1 m_2}{r^2}
$$
Where:
- $$ F $$ is the gravitational force between two objects.
- $$ G $$ is the universal gravitational constant, approximately $$ 6.67 \times 10^{-11} \, \text{N m}^2/\text{kg}^2 $$.
- $$ m_1 $$ and $$ m_2 $$ are the masses of the two objects.
- $$ r $$ is the distance between their centers.
How Does This Work?
Let’s break this down with an example. Imagine you have two objects: a basketball (mass = 0.6 kg) and a bowling ball (mass = 7 kg). If they are placed one meter apart, you can calculate the gravitational force between them using Newton’s formula.
- Calculate the product of their masses:
$$
m_1 \times m_2 = 0.6 \times 7 = 4.2 \, \text{kg}^2
$$ - Use the distance:
Since they are one meter apart, you use $$ r = 1 $$. - Plug into the equation:
$$
F = G \frac{4.2}{1^2} = (6.67 \times 10^{-11}) \times 4.2
$$
This will give you a very small force because even though both objects have mass, they are not massive enough to exert significant gravitational pull on each other at that distance.
Why Is This Important?
Newton’s law explains why planets orbit stars and moons orbit planets. For example, Earth orbits the Sun because of the gravitational pull between them—an interaction that keeps us in a stable orbit year after year.
The Connection to Kepler’s Laws
Kepler’s laws of planetary motion described how planets move around the Sun, but it was Newton’s law that provided the underlying reason for those movements. By understanding gravity as a universal force acting on all masses, Newton helped explain why planets follow elliptical orbits as described by Kepler.
Real-World Applications
Newton’s Law of Universal Gravitation has practical applications in various fields:
- Satellite Orbits: Understanding how gravity works allows scientists and engineers to calculate satellite trajectories and ensure they remain in stable orbits around Earth.
- Space Missions: When planning missions to other planets, such as Mars rovers or Voyager probes, scientists use Newton’s laws to determine how much fuel is needed and what trajectory to take.
- Tides: The gravitational pull of the Moon and Sun affects ocean tides on Earth. Understanding this interaction helps predict tidal patterns important for navigation and coastal management.
Newton’s Law of Universal Gravitation is a cornerstone of physics that explains how objects in our universe interact through gravity. By establishing that every mass attracts every other mass with a force dependent on their masses and distance apart, Newton laid the groundwork for modern astrophysics and our understanding of celestial mechanics.
The Advent of Space Exploration
Fast forward to the 20th century—the dawn of space exploration began with significant milestones like the launch of Sputnik 1 in 1957. As space agencies started launching satellites and spacecraft, understanding orbital mechanics became essential for navigation and communication.
One notable application is in Global Positioning System (GPS) technology. GPS relies on satellites orbiting Earth that transmit signals to receivers on the ground. By triangulating these signals, GPS can determine precise locations anywhere on Earth.
Modern Applications of Orbital Mechanics
Today, orbital mechanics plays a vital role in various fields, impacting everything from space exploration to everyday technology. Let’s explore some key applications of this fascinating discipline.
1. Space Station Orbit
The International Space Station (ISS) orbits Earth at an altitude of about 250 miles (400 kilometers). Orbital mechanics ensures that the ISS remains in a stable orbit, allowing astronauts to conduct scientific research without interruption.
How It Works: The ISS travels at a speed of approximately 17,500 miles per hour (28,000 kilometers per hour), completing an orbit around Earth roughly every 90 minutes. This high-speed travel is necessary to balance the gravitational pull of Earth and the centrifugal force due to its motion. If the ISS were to slow down, it would fall back to Earth; if it were to speed up too much, it could escape Earth’s gravity altogether.
2. Planetary Exploration
NASA’s Mars Reconnaissance Orbiter is another excellent example of how orbital mechanics is applied in planetary exploration. This spacecraft uses precise calculations to maintain its orbit around Mars while studying the planet’s geology and climate.
Example: The Mars Reconnaissance Orbiter captures high-resolution images and gathers data about the Martian surface and atmosphere. By understanding its orbital path and making necessary adjustments, scientists can ensure that the orbiter collects valuable information about potential water sources and past climate conditions on Mars.
3. Satellite Communications
Orbital mechanics is crucial for satellite communications, ensuring that satellites remain in their designated orbits for effective communication with Earth-based stations. This technology enables everything from television broadcasts to internet services.
How It Works: Satellites are placed into specific orbits based on their purpose. For example:
- Geostationary satellites orbit at an altitude of about 22,236 miles (35,786 kilometers) above the equator, allowing them to stay fixed over one spot on Earth. This is ideal for weather forecasting and communication.
- Low Earth orbit (LEO) satellites, like those used for GPS, orbit much closer to Earth (around 100 to 1,200 miles or 160 to 2,000 kilometers), providing real-time data for navigation and location services.
4. Weather Forecasting
Meteorological satellites heavily rely on principles of orbital mechanics to provide accurate weather forecasts. These satellites are usually placed in geostationary orbits above the equator, where they can continuously monitor weather patterns over specific regions.
Example: By tracking cloud movements and temperature changes from space, meteorological satellites help predict storms and other weather events, providing crucial information for public safety.
5. Asteroid and Comet Tracking
Orbital mechanics is essential for tracking asteroids and comets that pass near Earth. Understanding their orbits allows scientists to predict their paths accurately and assess any potential threats they might pose.
How It Works: By calculating the gravitational influences of nearby planets and the Sun on these celestial bodies, astronomers can determine whether an asteroid might collide with Earth in the future. This information is vital for planetary defense efforts.
6. Interplanetary Travel
Planning missions to other planets involves complex calculations based on orbital mechanics. For instance, NASA’s missions to Mars require precise understanding of both Earth’s and Mars’ positions in their respective orbits.
Example: When launching a spacecraft to Mars, mission planners calculate the optimal launch window when both planets are favorably aligned. This ensures that the spacecraft can reach Mars using the least amount of fuel while maximizing travel efficiency.
The evolution of orbital mechanics has led to remarkable advancements in technology and our understanding of space. From maintaining the International Space Station’s orbit to enabling satellite communications and planetary exploration, orbital mechanics continues to be a fundamental discipline guiding modern science and engineering.
Conclusion
The evolution of orbital mechanics has been an incredible journey—from Kepler’s insightful laws in the 17th century to today’s advanced space exploration technologies. As we continue to explore space and push technological boundaries, Kepler’s laws remain fundamental principles guiding our understanding of how celestial bodies interact and move through our universe.
Disclosure/Disclaimer:
This article contains affiliate links, supporting our educational and informative contents creation.
We appreciate supporting us to create more value and fascinating contents here on our site for educational purposes only.





